Author: Denis Avetisyan
A new approach to portfolio optimization leverages reinforcement learning to maximize financial goals within defined timeframes, even in turbulent market conditions.
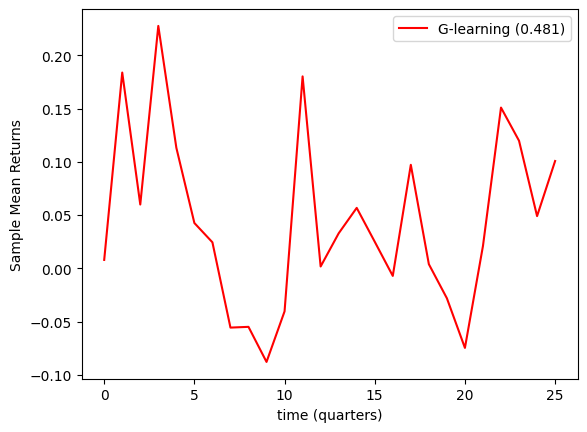
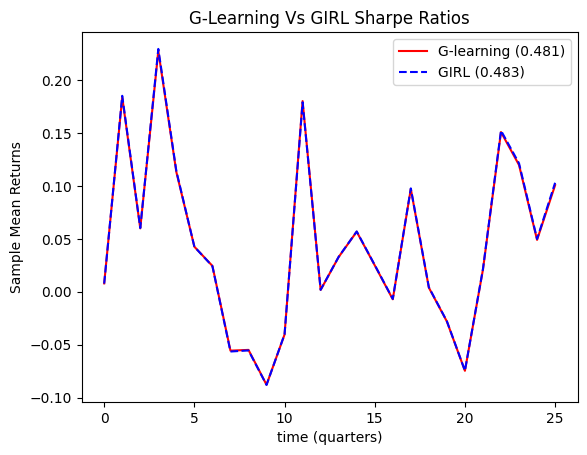
This review details how G-Learning, combined with the GIRL algorithm, effectively optimizes portfolio value and minimizes contributions while achieving a significant Sharpe ratio.
Achieving consistently high Sharpe ratios remains a key challenge in portfolio optimization, particularly amidst market volatility. This research, ‘Reinforcement Learning for Portfolio Optimization with a Financial Goal and Defined Time Horizons’, proposes an enhanced G-Learning algorithm, coupled with parametric optimization via GIRL, to maximize portfolio value while minimizing investor contributions. Results demonstrate a notable improvement, achieving a Sharpe Ratio of 0.483 in diversified portfolios-a significant gain over existing approaches. Could this approach unlock more robust and adaptive strategies for goal-based investing in dynamic financial landscapes?
Beyond Predictability: The Limits of Static Portfolio Theory
Classical portfolio optimization, exemplified by Modern Portfolio Theory, fundamentally depends on the analysis of past market performance to predict future outcomes. This reliance on historical data, while mathematically convenient, introduces a critical limitation: it assumes asset behavior will remain consistent over time. However, financial markets are demonstrably dynamic, influenced by evolving economic conditions, geopolitical events, and shifts in investor sentiment. Consequently, portfolios constructed solely on historical correlations and statistical properties may fail to capture emerging opportunities or adequately prepare for unforeseen risks. The static nature of these models struggles to account for changing volatility, the emergence of new asset classes, or structural breaks in market relationships, potentially leading to suboptimal investment strategies and missed potential gains. This inherent backward-looking approach underscores the need for more adaptive and forward-looking portfolio construction techniques.
The Sharpe Ratio, a cornerstone of portfolio evaluation, quantifies risk-adjusted return by dividing excess return – the return above the risk-free rate – by portfolio volatility. While widely used, this metric operates under limitations; it assumes investors primarily focus on maximizing return per unit of total risk, neglecting individual financial goals and time horizons. A retiree seeking stable income, for example, may prioritize minimizing downside risk over achieving the highest possible average return, a nuance the Sharpe Ratio doesn’t capture. Furthermore, the ratio is static, failing to adapt to evolving market conditions; a portfolio exhibiting a strong Sharpe Ratio in one economic climate may falter during periods of heightened volatility or shifting correlations. Consequently, reliance on the Sharpe Ratio as a sole determinant of portfolio suitability can be misleading, particularly when investor objectives extend beyond simple return maximization or when market dynamics undergo significant change.
Conventional portfolio construction frequently centers on static asset allocation, proving inadequate when faced with the realities of consistent savings and defined financial goals. Many established techniques assume a lump-sum investment, overlooking the impact of regular contributions – a cornerstone of long-term financial planning for most individuals. This limitation hinders the ability to precisely model wealth accumulation toward a specific future purchase, like a home or retirement, as the timing and amount of contributions significantly alter the projected outcomes. Consequently, portfolios optimized solely on risk-adjusted returns, such as those utilizing the Sharpe Ratio, may fall short of achieving targeted objectives, necessitating more sophisticated approaches that dynamically adjust asset allocation based on both market performance and the investor’s ongoing contribution schedule and evolving financial needs.
Rewriting the Rules: Reinforcement Learning for Portfolio Optimization
Reinforcement Learning (RL) provides a portfolio optimization framework where an agent iteratively learns to maximize cumulative rewards through interaction with a defined market environment. This environment simulates historical or synthetic market data, providing the agent with state information – typically consisting of asset prices, volumes, and technical indicators. The agent then selects actions – buy, sell, or hold – for various assets. Each action transitions the environment to a new state and generates a reward, quantifying the immediate performance of the portfolio. Through repeated interactions and leveraging algorithms like Q-learning, the agent refines its policy – the mapping from states to actions – to identify strategies that consistently generate high returns while adhering to specified risk constraints. This differs from traditional optimization techniques by removing the need for explicit mathematical models of market behavior, allowing the agent to adapt to complex and dynamic conditions.
G-Learning extends the principles of Q-Learning by incorporating probabilistic modeling of state transitions, addressing limitations inherent in deterministic environments. While Q-Learning estimates the optimal action-value function $Q(s,a)$, G-Learning estimates the optimal policy directly through a policy gradient approach. This is achieved by maintaining a probability distribution over possible actions for each state, allowing the agent to explore a wider range of strategies and adapt to stochastic market conditions. Specifically, G-Learning updates the policy parameters based on the gradient of the expected cumulative reward, leading to more robust decision-making in the presence of uncertainty and potentially higher long-term returns compared to deterministic approaches.
G-Learning employs a Reward Function, denoted as $R(s, a)$, to assess the value of transitioning to a new portfolio state, ‘s’, after executing action ‘a’. This function assigns a scalar value representing the immediate benefit or cost associated with that transition, considering factors like portfolio return, transaction costs, and risk exposure, often quantified using metrics like Sharpe Ratio or Sortino Ratio. The agent then utilizes this reward signal to learn an optimal policy – a mapping of states to actions – that maximizes the cumulative discounted reward over a defined time horizon. By explicitly defining the desirability of different portfolio states through the Reward Function, G-Learning enables the agent to balance maximizing returns with managing downside risk, leading to more robust and stable portfolio strategies.
Decoding Intent: Inferring Investor Objectives
Inverse Reinforcement Learning (IRL) addresses the challenge of determining the objectives driving observed decision-making. In the context of financial markets, IRL algorithms analyze investor actions – specifically, trade executions and portfolio rebalancing – to infer the underlying reward function that motivates those actions. Unlike traditional reinforcement learning, which requires a predefined reward function, IRL estimates this function from behavioral data. This is achieved by formulating the investor’s behavior as an optimization problem and identifying the reward function that best explains the observed choices. The inferred reward function can then be represented mathematically, allowing for quantitative analysis of investor preferences regarding risk, return, and time horizons. The resulting function isn’t a direct measurement of stated preferences, but rather an empirically derived model of behavior, offering insights into implicit objectives.
The GIRL algorithm integrates Inverse Reinforcement Learning (IRL) with the G-Learning framework to personalize portfolio optimization. Specifically, GIRL employs IRL to estimate the parameters defining an investor’s reward function – quantifying preferences for risk, return, and investment horizons – directly from observed trading data. These learned parameters are then incorporated into the G-Learning process, which iteratively refines the optimal trading strategy. This allows the system to move beyond pre-defined reward structures and dynamically adapt to individual investor preferences, resulting in portfolio recommendations tailored to specific financial goals and risk tolerance levels. The algorithm’s efficacy relies on accurately inferring the reward function from limited behavioral data, a challenge addressed through various IRL techniques incorporated within the GIRL framework.
Combining Inverse Reinforcement Learning (IRL) with G-Learning enables portfolio optimization strategies to transition from broadly applicable, generic approaches to solutions tailored to individual investor objectives. Traditional portfolio optimization often relies on predefined reward functions – such as maximizing Sharpe ratio – that may not accurately reflect a specific investor’s risk tolerance, investment horizon, or unique financial goals. IRL addresses this limitation by inferring the investor’s implicit reward function directly from their observed trading behavior and portfolio choices. This learned reward function is then integrated into the G-Learning algorithm, which iteratively refines the investment strategy to align with the inferred preferences, resulting in a personalized portfolio construction process that can accommodate nuanced and complex financial aims beyond standard metrics.
Beyond Prediction: Navigating Market Realities
Market fluctuations inherently pose a threat to portfolio returns, but recent advancements in algorithmic trading offer a powerful countermeasure. Sophisticated techniques, such as G-Learning, represent a class of reinforcement learning algorithms capable of dynamically adjusting investment strategies in response to evolving market conditions. Unlike static approaches, G-Learning continuously refines its decision-making process by learning from past experiences and predicting future market behavior, effectively mitigating risk. This adaptive capability allows the algorithm to navigate volatility, identifying opportunities even amidst downturns and optimizing asset allocation to maximize returns without relying on pre-defined rules or human intervention. The result is a portfolio that demonstrates resilience and consistently seeks the most favorable outcomes, even within a highly unpredictable financial landscape.
To effectively train artificial intelligence for financial trading, researchers utilize simulations grounded in established financial models. Geometric Brownian Motion, a stochastic process describing asset price evolution, serves as a cornerstone for these virtual markets. This model, mathematically represented as $dS = \mu S dt + \sigma S dW$, captures the random, yet trend-like, behavior observed in real-world asset prices, where $\mu$ represents the expected return, $\sigma$ the volatility, and $dW$ a Wiener process embodying randomness. By generating synthetic market data based on Geometric Brownian Motion, reinforcement learning agents can explore countless trading scenarios, learning optimal strategies without the risk of actual capital loss. This simulated environment allows for rigorous testing and refinement of algorithms, ensuring their robustness and performance before deployment in live markets, ultimately enhancing the potential for maximizing portfolio returns amidst inherent market uncertainty.
Recent investigations have yielded a reinforcement learning strategy capable of achieving a Sharpe Ratio of 0.483 within a dynamic and unpredictable market environment. This metric, a key indicator of risk-adjusted return, suggests the approach effectively maximizes portfolio value while simultaneously reducing the need for frequent financial contributions. The system learns to navigate market fluctuations, optimizing asset allocation to consistently generate positive returns relative to the inherent risk. This performance highlights the potential of intelligent algorithms to not only withstand market volatility but to actively capitalize on it, offering a compelling alternative to traditional portfolio management techniques and suggesting a pathway toward more efficient capital growth with minimized investor input.
The study’s success in navigating volatile markets through G-Learning and the GIRL algorithm isn’t merely about achieving a high Sharpe ratio; it’s a testament to the power of iterative refinement. This aligns perfectly with John Dewey’s assertion that “Education is not preparation for life; education is life itself.” The algorithm, much like a learning organism, doesn’t passively await optimal conditions; it actively tests boundaries, adjusts strategies based on feedback, and continuously evolves. The researchers effectively built a system that doesn’t just predict market behavior, but responds to it, embodying a truly experiential approach to portfolio optimization. This constant cycle of action and reflection is at the heart of both effective investing and meaningful learning.
Beyond the Horizon
The demonstrated efficacy of G-Learning within a goal-oriented portfolio framework isn’t a destination, but a carefully constructed lever. This work exposes the inherent limitations of static benchmarks-Sharpe ratio, while useful, merely quantifies a past relationship, a ghost in the machine. Future iterations must confront the non-stationarity of financial landscapes, acknowledging that the ‘rules’ governing asset behavior are themselves evolving, perhaps even intentionally obscured. The algorithm’s success in volatile markets invites a deliberate provocation: how thoroughly can one deconstruct the very notion of ‘risk’ before performance becomes indistinguishable from chance?
A compelling, yet largely untouched, avenue lies in extending the Markov Decision Process beyond purely financial instruments. Incorporating external, seemingly unrelated data – geopolitical indicators, sentiment analysis from unconventional sources, even subtle shifts in network topology – could reveal predictive patterns currently masked by conventional modelling. This isn’t about achieving perfect foresight, but about building a system that expects imperfection, and actively probes the boundaries of predictability.
Ultimately, the true test won’t be maximizing returns within defined horizons, but building an architecture resilient enough to abandon those horizons when necessary. The algorithm shouldn’t simply respond to chaos; it should anticipate it, and actively seek out the cracks where the established order begins to unravel. Such a system wouldn’t merely optimize a portfolio, but actively redefine the game itself.
Original article: https://arxiv.org/pdf/2511.18076.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- DOGE PREDICTION. DOGE cryptocurrency
- Calvin Harris Announces India Debut With 2 Shows Across Mumbai and Bangalore in November: How to Attend
- EQT Earnings: Strong Production
- The Relentless Ascent of Broadcom Stock: Why It’s Not Too Late to Jump In
- Docusign’s Theatrical Ascent Amidst Market Farce
- TON PREDICTION. TON cryptocurrency
- HBO Boss Discusses the Possibility of THE PENGUIN Season 2
- Ultraman Live Stage Show: Kaiju Battles and LED Effects Coming to America This Fall
- Why Rocket Lab Stock Skyrocketed Last Week
- The Dividend Maze: VYM and HDV in a Labyrinth of Yield and Diversification
2025-11-25 20:58